
Artists are sometimes surprised to see one application of paint barely hide the drawing or painting underneath and another color completely mask all that was below. Some wonder why sometime after they completed a painting, they begin to see lines of the sketch that before were completely unnoticed. (This effect is called pentimento.) Other artists wishing to apply a beautiful glaze are frustrated when the glaze kills the color below. These are common problems experienced by all painters at one time or another, but they little understand the reasons.
Given the same thickness of applied paint film, not all paints are equally opaque (or transparent). We call this hiding strength or covering power. The hiding strength (or opacity) of paint is primarily influenced by the difference in the refractive indices of the pigment and the medium, particle size and dispersion of the pigment (i.e., particle shape and degree of aggregation of the particles), the proportion of pigment in the vehicle (i.e., pigment volume concentration or PVC) and the thickness of the applied film. These factors determine the opacity of a particular paint. In this article, we will focus on the refractive index of pigments and paint vehicles; the other factors were considered in another article, “Do Natural Pigments Offer More to the Modern Painter?”
Paints contain tiny pigment particles suspended in a binder, such as oil. We are accustomed to regard some pigments as transparent or translucent and others as opaque. Pigments usually considered to be opaque are translucent in a highly refractive medium. Using a medium of high refractive index, it can be shown that the most opaque colors, even lead white, appear transparent. This demonstrates that a pigment’s hiding strength or opacity can be lost through a change in the conditions surrounding the pigment or, in the case of paint, a change in the binder.
Pigment particles absorb specific wavelengths of light, creating colored paints, or they may reflect, refract and scatter all wavelengths of light, appearing white to our eyes. Let’s consider what happens when light encounters a layer of paint containing only pigment particles.
The Behavior of Light Passing Through Substances
To help us understand the opacity of pigment in paint, we will need to consider the behavior of white light on substances. We think of a sheet of glass as a transparent substance through which light passes without obstruction. Yet, if we look out of our window at night, we get a nearly perfect mirror image of the interior of our home.
As beams of light pass from the air to glass, they are impeded, so some light is reflected while parts are transmitted. If the beam of light, called incident light, hits the glass at an angle, the transmitted beam is bent out of its path upon entering it to shorten its path (fig.1).

Fig. 1. When light passes through a substance, some is reflected and some transmitted. Transmitted light is refracted as it encounters a material, such as liquid or solid, that impedes its velocity through it.
Light travels at a constant velocity in a vacuum, but its velocity is slower when it travels through a substance. So, in our example, when the light passes from less dense air to denser glass, its velocity is slowed down; the beam of light is bent or refracted. The amount of refraction is the measure of impediment given by the substance to the beam of light. In our example, we can substitute the glass for other substances, such as water, oil, or pigments, and find that light is impeded for each substance. (The degree to which light is bent is also dependent upon other factors, such as the temperature of the substance and the wavelength of the light.) The proportion between the reflected light and the light that enters the substance and is refracted also varies.
The ratio of the velocity of light in a vacuum to the velocity of light in another substance is expressed as the index of refraction or refractive index. It is measured by the angle at which the ray of light is bent. To determine this ratio, one must know the angle of incidence or the angle between the ray of light entering the substance and a line perpendicular to its surface, and the angle of refraction, defined as the angle between the refracted ray and the perpendicular to the surface. In mathematical terms, if i is the angle of incidence and r is the angle of refraction, then the refractive index is N, expressed as follows:
| sine i | |
| N = | ------- |
| sine r |
By definition, the refractive index of a vacuum is 1. In practice, air makes little difference to the refraction of light with an absolute refractive index of 1.0008, so the value of the absolute refractive index can be used assuming the incident light is in the air. Since light slows down when it enters a substance, so the refractive index will always be greater than 1. Most minerals have refractive indices between 1.32 and 2.40, with values between 1.50 and 1.80 (Jones, 1980).
| Material | Refractive Index |
| Air | 1.0008 |
| Water | 1.3330 |
| Glass, soda-lime | 1.5100 |
| Ruby | 1.7600 |
| Diamond | 2.4170 |
The amount of light rays that may be bent, as shown in Figure 1, depends upon the substance it enters. This change in direction becomes smaller as the angle of incidence decreases. Eventually, when light is perpendicular to a surface, it will not bend. The angles at which light is refracted is a constant. The constant N (refractive index) for a pigment depends on the difference between the velocity of light in the surrounding medium and the pigment. It is a characteristic constant for every material, including gases, liquids, and solids. We cannot observe the change in the velocity of light in small pigment particles. Still, we can observe a change in the direction of propagation of the light and calculate or estimate the refractive index.
The refractive index is easy to learn, but things aren’t quite that simple. The refractive index of a pigment particle is not necessarily the same in all directions. Most pigments are composed of crystals that have definite shapes and are classified into different systems. In cubic crystals, light travels at the same speed in all directions within the crystal, which is said to be isotropic. Light does not travel at the same speed in all directions within substances that belong to the five other crystal classes; these are said to be anisotropic. In addition, anisotropic substances are divisible into two types:
Uniaxial are substances that have two refractive indices (tetragonal and hexagonal system minerals);
Biaxial are substances characterized by three refractive indices (triclinic, monoclinic, and orthorhombic system minerals).
The most important thing to remember is that a substance that has a higher refractive index is a substance that impedes the velocity of light or offers more resistance to it. Therefore a larger proportion of the light will be scattered.
Let’s return to our example of the light beam passing into a substance. Consider what happens when a light beam passes from a substance of one refractive index to another substance of another refractive index.
If a beam of light passes from a substance like air with a low refractive index to a substance of higher refractive index, such as water, that impedes the passage of light, part of the light will be reflected at the interface or boundary of the two substances (Fig. 1). Light changes speed as it moves from air to water so that it also experiences refraction. In our consideration of pigments, refraction is most important. Suppose we view water inside a shallow glass dish. In that case, some of the light passing through the water and entering the glass, which has a higher refractive index than water, is reflected and some refracted (Fig. 2). We get two reflections and two refractions; one at the surface of the water, and another at the boundary of the water and glass.

Fig. 2. Light passes through two substances, one with a low refractive index and the other with a high refractive index.
Typically, solid substances have higher refractive indices than liquids, so if we suspend a sheet of glass in a shallow dish of water, we will see a strong reflection and high refraction at their interface because of the differences in their refractive indices (Fig. 3).
Instead of a sheet of glass of higher refractive value than water, we place a transparent sheet of another material with a low refractive index, like gelatin; we shall get a comparably feeble reflection at the boundary of the water and gelatin.
If instead of removing the glass, we replace the water with a liquid of a higher refractive index, the same refractive index as glass, there will be no reflected light at the meeting of the liquid and glass.

Fig. 3. Light passing through a liquid of low refractive index and then through a glass plate, illustrating how pigment particles reflect and transmit light in a medium.
Let us summarize what we’ve learned about the behavior of light. Light is reflected at the boundary when a ray of light passes from a substance of low refractive index to a substance of high refractive index; the amount of light scattered being greater, the more significant the difference between their respective refractive indices.
The Behavior of Light in Paint
Now we will approximate the conditions we find in paint. Let us return to our example of the glass sheet suspended in a liquid. We now break the glass into pieces and grind it into a fine powder. This powder appears white and opaque, but if we were to examine a glass particle in a microscope, we would see that it is transparent. The reason is that the light reflected from the many facets of glass particles is scattered, and it is scattered light that produces opacity.
Now put the powdered glass in a container, and fill the container with water. The differences between water and glass refractive indices are not as significant as between air and glass. As you fill the container with water, the powder glass does not scatter so much light. It becomes partly translucent. If the liquid had the same refractive index as glass, the glass would be almost invisible. Though water is not of such a high refractive index as glass, it is much higher than air, and as we see the glass by scattered reflection, if the reflection no longer takes place, the glass disappears. This is the same phenomenon we observe when we wet an opaque substance, it appears darker in color.
We will repeat what was said earlier: Some pigments we consider transparent, translucent, and others opaque. Pigments usually considered opaque are transparent in a highly refractive medium. Using a medium of high refractive index, it can be shown that the most opaque colors, even lead white, appear transparent.
Most light enters the paint surface and then passes through the randomly shaped and oriented pigment particles. These particles are translucent and don’t absorb much light, but they have a refractive index higher than the surrounding medium.
What happens to light passing through one of these pigment particles? A portion of the light reflects at the surface of each pigment particle. Again, changes in the speed of light as it enters the pigment particle causes the light to bend or refract. The light is impeded trying to pass through the particles, even though the particles may not absorb much light. The light’s path changes at the surface, and some of it is reflected from the paint.
The random shape and orientation of the pigment particles give a paint film of white pigment its white appearance. If all of the pigment particles were instead flat disks that lay parallel to the paint’s surface, like coins lying flat on the bottom of a shallow pan of water, the paint would reflect the light much like a mirror rather than form a white surface. The reason is that the flat disks would reflect light directly from the paint as a mirror. The paint film would appear like a mirror rather than the color we perceive as white. The random surfaces of the pigment particles give white paint its diffuse glow. A narrow beam of light hitting white paint scatters in all directions, while a beam hitting the mirror bounces back as a narrow beam.
If the pigment particles had precisely the same index of refraction as the medium that holds them, how would this alter the appearance of the paint? The paint would appear translucent. Light passes through it unaffected without changes in the refractive index between the pigment and the medium. Although some light will reflect at the boundary of the air and paint layer, whatever light enters the paint will continue through it to the ground under the paint. The paint will appear translucent. When mixed with linseed oil, some pigments, such as chalk, lose their hiding strength and appear translucent because they have a refractive index close to that of linseed oil.
White pigments typically have a refractive index above 2—a high ability to refract light that strikes it obliquely and a high ability to reflect light. IN artists’ paints, there are only a few white pigments with refractive indices above 2: titanium dioxide (TiO2), lead white (basic lead carbonate, 2PbCO3•Pb(OH)2), zinc oxide (ZnO) and zinc sulfide (ZnS). On the other hand, many white pigments have refractive indices of less than two and, in oil and acrylic paint, are considered to be extender or filler pigments. Common ones are silica (SiO2), chalk (calcium carbonate, CaCO3), barite (barium sulfate, BaSO4), and gypsum (calcium sulfate hemihydrate, CaSO4•0.5H2O). If you look at the table of refractive indices, substances with higher refractive indices have greater opacity or covering power because of their high refractive index.
| Color | Pigment | Refractive Index |
| Blues | Azurite | 1.73–1.84 |
| Indigo (natural dye) | 1.49–1.52 | |
| Smalt | 1.49–1.52 | |
| Lazurite (natural ultramarine) | 1.50 | |
| Vivianite (blue ocher) | 1.58–1.70 | |
| Greens | Chrysocolla | 1.58–1.60 |
| Dioptase | 1.64–1.71 | |
| Glauconite (green earth) | 1.62 | |
| Malachite | 1.65–1.90 | |
| Verdigris (basic copper acetate) | 1.53–1.56 | |
| Volkonskoite | 2.50 | |
| Yellows | Gamboge (organic resin) | 1.58–1.59 |
| Indian yellow (organic resin) | 1.67 | |
| Jarosite | 1.71–1.82 | |
| Massicot (litharge, lead monoxide) | 2.50–2.61 | |
| Goethite (yellow ocher) | 2.00–2.40 | |
| Orpiment | 2.40–3.02 | |
| Reds | Cinnabar | 2.81–3.15 |
| Hematite (red iron oxide) | 2.78–3.01 | |
| Realgar | 2.46–2.61 | |
| Red lead (minium or lead tetroxide) | 2.42 | |
| Vermilion | 2.82–3.15 | |
| Browns | Goethite (brown ocher) | 2.08–2.40 |
| Siderite | 1.57–1.78 | |
| Sienna, burnt | 1.85 | |
| Sienna, raw | 1.87–2.17 | |
| Umber, burnt | 2.20–2.30 | |
| Umber, raw | 1.87–2.17 | |
| Whites | Chalk (whiting, calcium carbonate) | 1.51–1.65 |
| Gypsum, anhydrite (calcium sulfate anhydrate) | 1.57–1.61 | |
| Gypsum, hemihydrate (gesso, calcium sulfate hemihydrate) | 1.52–1.53 | |
| Titanium dioxide (anatase) | 2.27 | |
| Titanium dioxide (rutile) | 2.71 | |
| Lead white (basic lead carbonate) | 1.94–2.09 | |
| Zinc oxide | 2.00–2.02 | |
| Blacks | Carbon black | (opaque) |
Since there is little or no light absorption for white pigments, the hiding power of white paints depends entirely on the scattering of the incident light. The higher the refractive index of the pigment relative to that of the medium, and the nearer the particle size to the optimum, the greater the scatter and the greater the opacity of the paint.
The hiding power of a paint containing a colored pigment is also dependent on the ability of the pigment to absorb light and scatter it due to its refractive index and particle size distribution. With black pigments, good hiding power is obtained owing to the almost complete absorption of light and refractive index, contributing only little to the effect. For other colored pigments, both of these properties, absorption and scatter, are wavelength-dependent, and the end effect is a complex combination of all the various factors involved.
All inorganic pigments have high refractive indices; hence, when used to color paint give high opacity. Such colors from inorganic pigments generally include white, black, yellow, red, and green oxides. Depending on the proportions, colors comprising combinations of inorganic and organic pigments may have high opacity.
Changing the Opacity of Oil Paint
Peter Paul Rubens, The Miracles of Saint Francis of Paola, oil on panel, 975×772 mm, c. 1627–8, J. Paul Getty Museum. Click on the image to see a detail of the pentimento.
The refractive index of substances is not absolute but changes with time. For example, as linseed oil ages, the refractive index increases from 1.479 to over 1.525 in about ten years. It has been measured as high as 1.58 in several hundred years old paintings. This causes oil paint to lose its covering power and become more transparent with time. This phenomenon can be seen in such old master paintings as the pentimento in the upper left of Peter Paul Rubens’ modello, The Miracles of Saint Francis of Paola. The two columns appear superimposed on top of an archway. The archway was painted over, but it reappeared as the painting aged, and the layers of oil paint became transparent.
To avoid this effect, artists must be aware of the changes in refractive index, use pigments with high refractive indices, and apply sufficiently thick layers of paint.
Conclusion
When selecting a pigment, it is essential to know how opaque it is in the paint binder. Depending on the paint’s desired effect, such as scumbles or glazes, you will need to use either opaque or transparent pigments. For underpainting, you will typically need an opaque pigment and one with a lower refractive index for the final layers. The opacity of a pigment depends mainly on the difference between the refractive indices of the pigment and the binding materials, the granularity of the pigments, and the degree of pigment concentration in the binding medium.
Appendix
| Material | Refractive Index |
| Water | 1.333 |
| Linseed oil, refined, fresh* | 1.479 |
| Linseed oil, aged ten years | >1.520 |
| Egg yolk, dried | 1.525 |
| Artificial Resins | |
| Polyvinyl acetate (PVA) | 1.473 |
| Acrylic (methyl methacrylate) | 1.489–1.498 |
| Acrylic copolymer (methyl methacrylate styrene) | 1.558–1.574 |
| Natural Resins | |
| Damar, Singapore |
1.515 |
| Rosin, wood, Grade M | 1.525 |
| Rosin, ester | 1.496 |
| Shellac, bleached | 1.534 |
| Mastic | 1.536 |
| Canada balsam | 1.530–1.540 |
| Sandarac | 1.545 |
* It is well known that the refractive index, viscosity, and molecular weight of linseed oil and other non-conjugated oils decrease due to heat processing.
Source: (Gardner 1972)
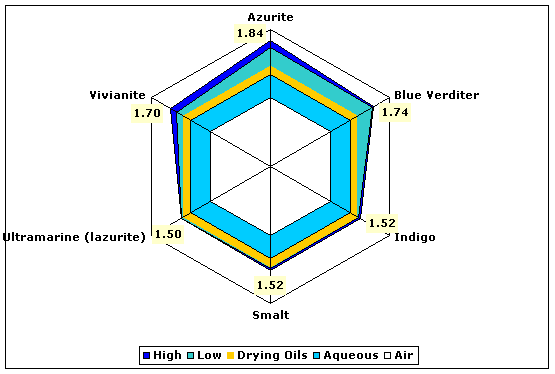
Fig. 4. Refractive indices of various blue pigments compared to aqueous and drying oil mediums.

Fig. 5. Refractive indices of various brown pigments compared to aqueous and drying oil mediums.
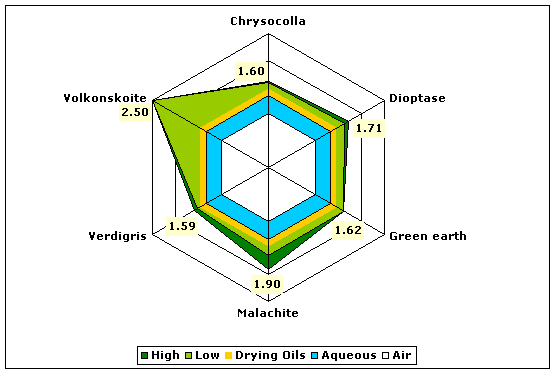
Fig. 6. Refractive indices of various green pigments compared to aqueous and drying oil mediums.
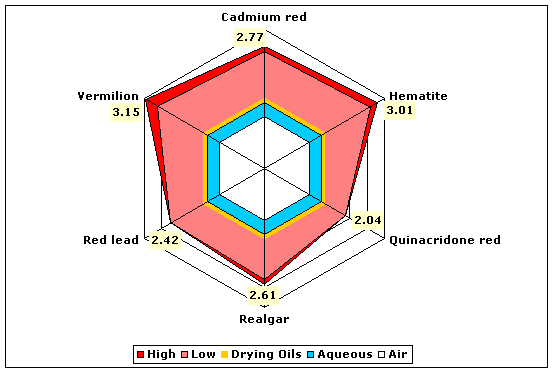
Fig. 7. Refractive indices of various red pigments compared to aqueous and drying oil mediums.
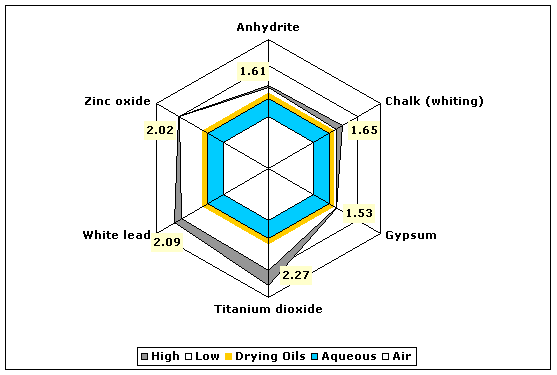
Fig. 8. Refractive indices of various white pigments compared to aqueous and drying oil mediums.
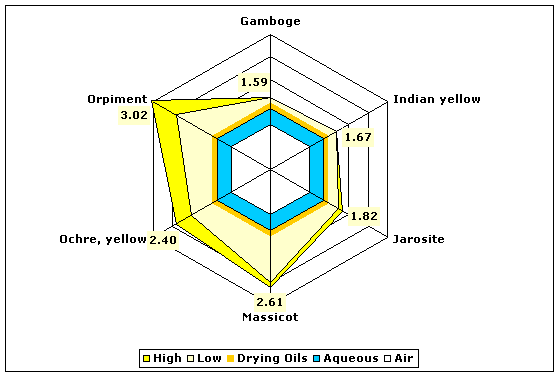
Fig. 9. Refractive indices of various yellow pigments compared to aqueous and drying oil mediums.
The following is based on color effects in Artists Handbook of Materials and Techniques by Ralph Mayer (Mayer 1985).
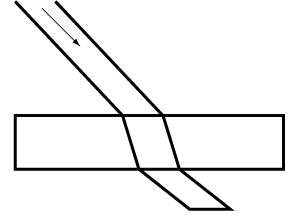
Refraction of light. A light ray passing through a sheet of glass or other transparent material bends (is refracted) and takes a shortcut. The angle of refraction varies with each substance and increases according to the power of each substance to impede light.
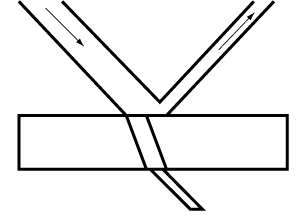
Transmission and reflection of light. Under average conditions, a certain amount of light is reflected from the surface of clear glass as from a mirror. The proportions of light reflected and transmitted vary according to the nature of the substance, the surrounding conditions, and in many cases, the angle from which the surface is viewed.
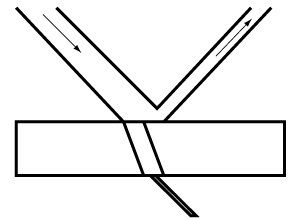
Absorption of light. Thin, translucent milk glass or other semi-opaque material transmits less light than transparent material. In this instance, some light is reflected, and some are absorbed. The more the light is impeded and absorbed, the greater the opacity.
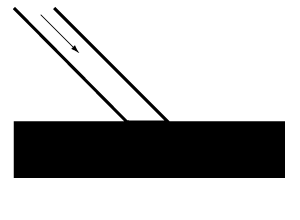
Dark surfaces. The most significant amount of light absorption, accompanied by the slightest reflection, occurs when light falls on a dead mat, an intensely black surface. Other issues being equal, a brilliant white surface will reflect the most light, and as it is tinted, the amount of reflection will decrease according to the depth of color.
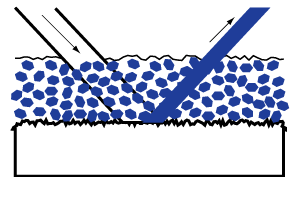
White grounds. When a layer of paint composed of pigment particles and binder is coated on a white ground, the resulting reflection of light contributes brilliance and luminosity, which are altogether lacking when the painting is done on a black ground.
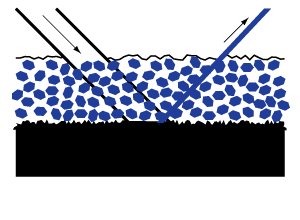
Colored and dark grounds. Any coloration of the ground will tend to decrease the amount of reflection, and the more translucent the coating is or becomes, the more the brightness of the resulting painting will be affected.
References
F. Donald Bloss, An Introduction to the Methods of Optical Mineralogy, New York: Holt, Rinehart and Winston, 1961, pp. 6, 131–142, 200–203.
Robert L. Feller, editor, Artists Pigments: A Handbook of Their History and Characteristics, Vol. I, New York: Oxford University Press, pp. 289–291.
Henry A. Gardner, George G. Sward, Paint Testing Manual, ASTM International, January 1, 1972, p. 79.
Rutherford J. Gettens and George L. Stout, Painting Materials: A Short Encyclopedia, New York: D. Van Nostrand Co., 1942, republished New York: Dover Publications, 1966, pp. 147–148.
Norris W. Jones and F. Donald Bloss, Laboratory Manual for Optical Mineralogy, Minneapolis, Minnesota: Burgess Publishing Co., 1980, pp. 3-1-3-5.
A. P. Laurie, The Painters Methods and Materials, New York: Dover Publications, 1988, pp. 102–110.
Ralph Mayer, The Artists Handbook of Materials and Techniques, 5th edition, New York: Viking Press, 1985, pp. 159–161.
H. E. Merwin, “Optical Properties and Theory of Color of Pigments and Paints,” Proceedings of the American Society for Testing Materials, XVII (1917), pp. 494–530.
Alexander N. Winchell and Horace Winchell, Elements of Optical Mineralogy: An Introduction to Microscopic Petrography, Part II Description of Minerals, 4th edition, New York: Wiley and Sons, 1951.












